1 . (单选题) 如图所示,甲、乙两人在一个长 100 米,宽5 0 米的 矩 形操场行走,甲 在 乙 前方 5 0 米 ,如两人以相同的速度顺时针行走,问 以下哪个 函数图最能反应时间(x轴)与甲、乙两人直线距离(y轴)之间的关系。

A.
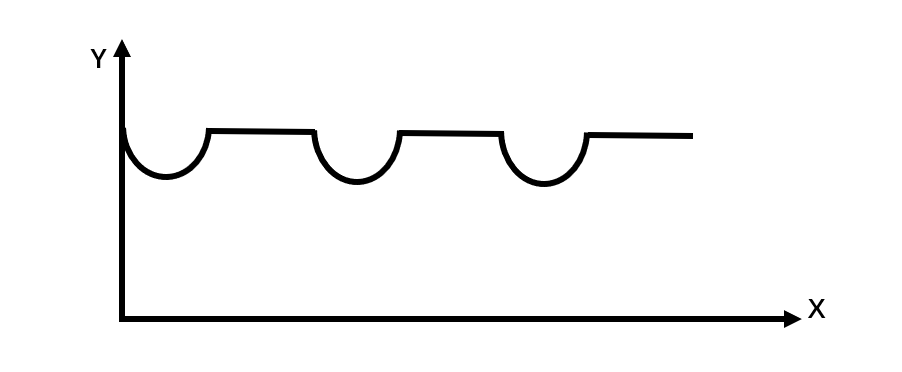
B .
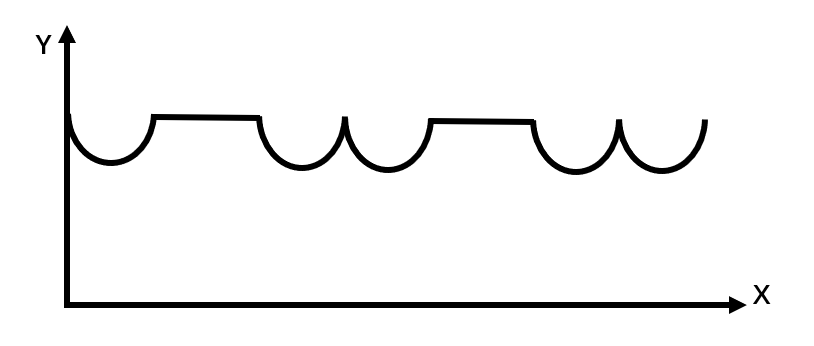
C.
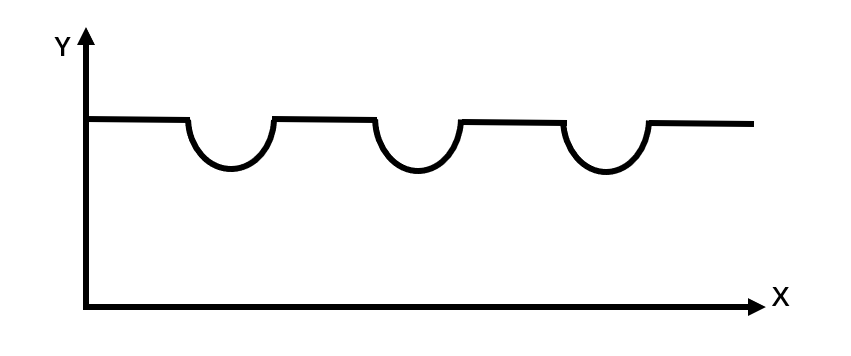
D.

【答案】 B
【解析】 第一步,本题考查 数学运算 知识点中的 函数 问题。
第二步, 采用描点法分析,(1)当甲、乙两人往前走1 0 米,两人相距距离 米,
( 2 )当甲、乙两人往前走 20 米,两人相距距离 米, (3) 当甲、乙两人往前走 25 米,两人相距距离 米, 通过这三组数据分析,两人相距距离不是一元一次方程函数图, 因此可知两人一开始相距直线距离是一个抛物线,结合选项排除C D 。
第 三 步, (3)当甲、乙两人往前走5 0 至1 00 米时,两人在矩形的长1 00 米行走,是一个直线运动过程。(4)1 00 米至1 50 米时,又是一个抛物线运动过程,1 50 米至2 00 米时,也是一个抛物线过程,结合选项排除A,选择B。
因此,选择 B 选项。
【拓展】
【标签】
【知识点】 函数问题
【难度】中等
【命题人】0 13915 戴世特
2 .(单选题) 用相同的 两瓶 容器 分别 装满浓度为 3 0 %的氯化钠溶液和浓度为1 0 %的氯化钠溶液,现 用这两种溶液 配制出同规格的 半瓶浓度为 25 %的氯化钠溶液,问将剩余的两种氯化钠溶液混合在一起,得到的浓度 约 为( )。
A. 15 %
B. 17.6 %
C. 18.3 %
D. 21. 2 %
【答案】 C
【解析】 第一步,本题考查数学运算知识点中的 溶液混合型 。
第二步, 赋值每瓶溶液为1 00 g。配置半瓶浓度为2 5 %的溶液,设需要浓度为3 0 %的溶液x克,需要浓度为1 0 %的溶液y克,列出等式:x+y= 50 ; 30 %x+ 10 %y= 50 × 25 %。求出x= 37.5 (克),y= 12.5 (克)。
第三步, 浓度为3 0 %的溶液剩余6 2.5 克,浓度为1 0 %的溶液剩余8 7.5 克 ,求混合后的浓度: ≈ 18.3 % 。
因此,选择 C 选项。
【拓展】
【标签】
【知识点】 溶液问题
【难度】中等
【命题人】0 13915 戴世特
3 . (单选题) 一项工程,由甲单独完成需要1 0 0 天,由乙单独完成需要1 2 0 天,由丙单独完成需要 1 5 0 天。现按照第一天甲乙合作,第二天甲丙合作,第三天乙丙合作循环工作 , 工程完成一半时乙有事离开, 剩余工程由 甲 、 丙每 人 轮流 工作一天 完成 ,如此循环 ,整个工程完成 用时 ( )天 。
A. 60
B. 70
C. 80
D. 90
【答案】 D
【解析】 第一步,本题考查 循环周期问题 。
第二步, 第一步赋值 工程 总量为 6 00 , 分别求出甲的工作效率为6 00 ÷ 100 = 6 ;乙的工作效率为6 00 ÷ 120 = 5 ;丙的工作效率为6 00 ÷ 150 = 4 。
第二步, 求出甲乙、甲丙、乙丙3天的工作量:(6+ 5 )×1+( 6 + 4 )×1+( 5 + 4 )×1= 30 。即一个循环工作的量为3 0 ,完成工程一半需要经过3 00 ÷ 30 = 10 个循环,因此需要1 0 × 3 = 30 天。
第三步, 剩余3 00 量的工程由甲丙循环完成,即完成剩余工程需要3 00 ÷(6+ 4 )= 30 (周期),即3 0 × 2 = 60 天。因此完成整个工程需要3 0 + 60 = 90 (天)。
因此,选择 D 选项。
【拓展】
【标签】
【知识点】 循环周期问题
【难度】 中等
【命题人】0 13915 戴世特
4 . (单选题) 某大型机器需要定期检查,甲每8天检查一次,乙每1 0 天检查一次,丙每1 6 天检查一次,在2 020 年2月2 8 日三人同时对机器进行检查,问该年最后一次 三人 同时检查机器是( )。
A. 10 月2 4
B. 1 0 月2 5
C. 10 月2 6
D. 10 月2 7
【答案】 B
【解析】 第一步,本题考查 约数倍数问题 。
第二步, 三人同时检查机器即要满足8的倍数,也满足1 0 的倍数,还满足1 6 的倍数,先用短除法找出8、 10 、 16 的最小公倍数为8 0 ,即每过8 0 天三人同时检查机器。
第三步, 根据题目意思,该年是2 020 年为闰年,从年初到 2 月2 8 日已过3 1 + 28 = 59 (天),所以该年剩余3 66 - 59 = 307 (天),因此从2月2 8 日到该年最后一次检查机器的时间只需要过8 0 × 3 = 240 天。
第四步, 方法一:以每月最后的一天分析 经过的时间,从2月2 8 日 到 2 月2 9 日 经过1天 ,2月2 9 日 到3月3 1 日 经过3 1 天 , 再到4月3 0 日 经过3 0 天,到5月3 1 日 经过 3 1 天,到 6 月3 0 日经过3 0 天,到7月3 1 日经过3 1 天,到8月3 1 日经过3 1 天,到9月3 0 日经过3 0 天,目前一共经过2 15 天,只需要再过2 5 天即可,即1 0 月2 5 日三人同时检查机器。
方法二:该年还剩3 07 天,即2 40 天后再经过6 7 天到 12 月3 1 日,只有从1 0 月2 5 到1 2 月3 1 日才是经过6 7 天。
因此,选择 B 选项。
【拓展】
【标签】
【知识点】 约数倍数 问题
【难度】中等
【命题人】0 13915 戴世特
5. (单选题) 用大小两 种 不同的货车运输 13 6 箱货物, 已知 每辆大货车能装 16 箱货物,每 辆小货车能装 10 箱货物,每辆大货车的运输费用是4 4 0 元,每辆小货车的运输费用是2 80 元。 小李租用若干辆大小货车运输,每车满载且刚好运输完所有货物,问小李至少需要支付多少钱?
A. 37 6 0 元
B. 37 8 0 元
C. 3 80 0 元
D. 38 2 0 元
【答案】 A
【解析】 第一步,本题考查 方程法中的不定方程 。
第二步, 设租用x辆大货车,y辆小货车,根据题干信息, 每辆大货车装 16 箱货物,每辆小货车装 10 箱货物, 满载且运输完,列式为:1 6 x+ 10 y= 13 6 ,化简得8x+ 5 y= 68 。
第三步,用奇偶性和尾数法算出x与y的值。6 8 是偶数,8x是偶数,因此5y是偶数,所以5y尾数为0,因此8x尾数为8,得出x= 1 ,y= 12 第 一组解,或者x= 6 ,y= 4 第二组解。
第四步,当x= 1 ,y= 12 ,算出总费用1× 440 + 12 × 280 = 3800 (元) 。 当x= 6 ,y= 4 ,算出总费用6× 440 + 4 × 280 = 3760 (元),所以小李至少支付3 760 元。
因此,选择 A 选项。
【拓展】
【标签】
【知识点】 不定方程
【难度】 中等
【命题人】0 13915 戴世特










